Optimization Algorithms优化算法
觉得有用的话,欢迎一起讨论相互学习~
2.3 指数加权平均
举个例子,对于图中英国的温度数据计算移动平均值或者说是移动平均值(Moving average).
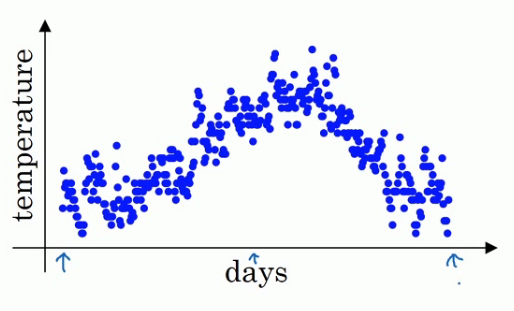

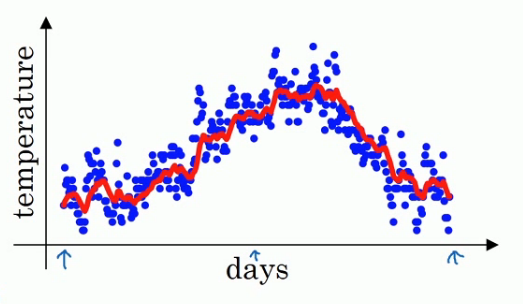
- 对于\(\theta\)的理解,你可以将其认为该数值表示的是\(\frac{1}{1-\beta}\)天的平均值,例如如果这里取\(\beta\)是取0.9,那么这个V值表示的是十天以来的温度的加权平均值.如果我们设置\(\beta\)值是0.98那么我们就是在计算50天内的指数加权平均,这时我们用图中的绿线表示指数加权平均值
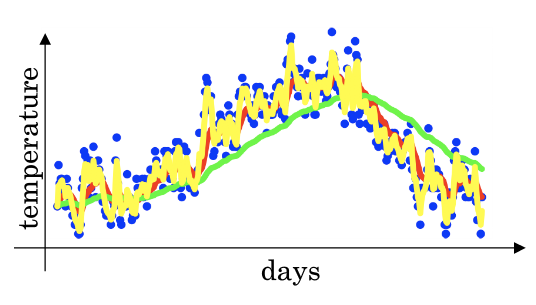
- 我们看到这个高值的\(\beta=0.98\)得到的曲线要平坦一些,是因为你多平均了几天的温度.所以波动更小,更加平坦.缺点是曲线向右移动,这时因为现在平均的温度值更多,所以会出现一定的延迟.对于\(\beta=0.98\)这个值的理解在于有0.98的权重给了原先的值,只有0.02的权重给了当日的值.
- 我们现在将\(\beta=0.5\)作图运行后得到黄线,由于仅平均了两天的温度,平均的数据太少,所以得到的曲线有更多的噪声,更有可能出现异常值,但是这个曲线能更快的适应温度变化,所以指数加权平均数经常被使用.
- 在统计学中,它常被称为指数加权移动平均值
2.4 理解指数加权平均
公式:\[V_{t}=\beta V_{t-1}+(1-\beta)\theta_{t}\]
- \(\beta\)为0.9时,得到的是红线,\(\beta\)为0.98,得到的是绿线,\(\beta\)为0.5时,得到的是黄线.
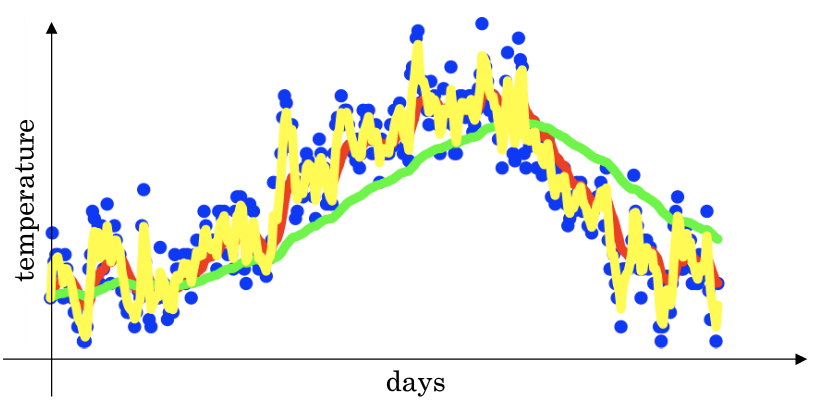
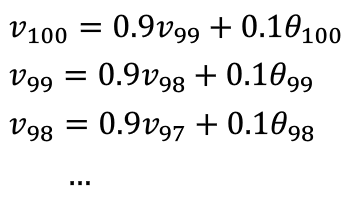
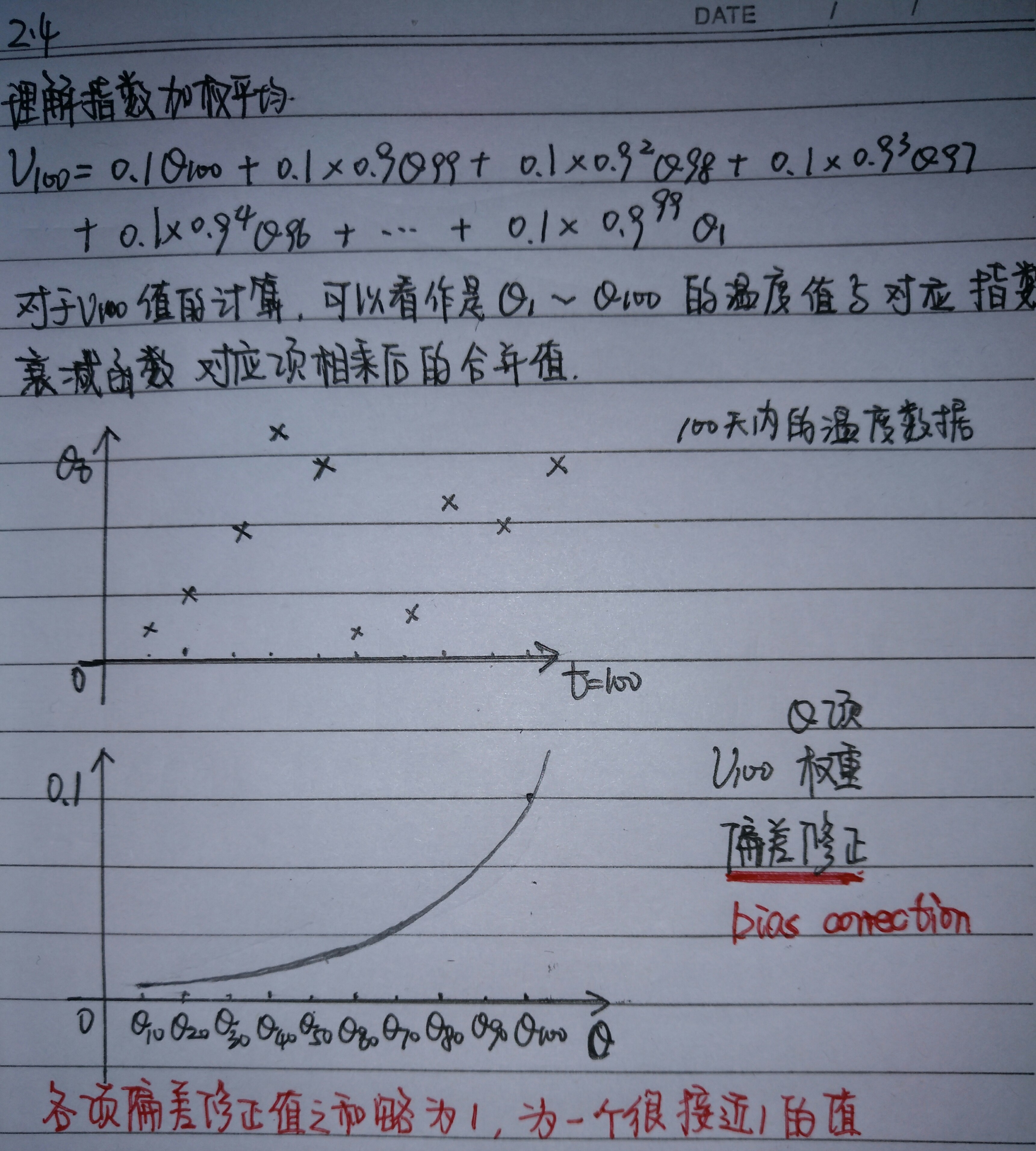
- 通过计算,我们发现\(0.9^{10}\approx\frac{1}{e}\approx0.35\),也就是说对于$\beta=0.9而言\(10天之后权重就会下降到\)\frac{1}{3}$
- 对于\(\beta=0.98而言,有0.98^{50}\approx\frac{1}{e}\approx0.35\),即50天之后权重就会下降到\(\frac{1}{3}\)
- 即有\[(1-\epsilon)^{\frac{1}{\epsilon}}\approx\frac{1}{e}\]
优势
实际处理数据时,我们会使用以下公式:
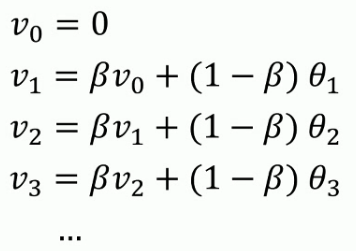
- 内存代码仅仅占用一行数字而已,不断覆盖掉原有的V值即可,只占单行数字的存储和内存.虽然不是最精确的计算平均值的方法,但是相比于原有的计算平均值需要保存所有数据求和后取平均的方法效率更高和资源占用率大大减小.所以在机器学习中大部分采用指数加权平均的方法计算平均值.
2.5 指数加权平均的偏差修正
当我们取\(\beta=0.98\)时,实际上我们得到的不是绿色曲线,而是紫色曲线,因为使用指数加权平均的方法在前期会有很大的偏差,为此我们引入了偏差修正的概念
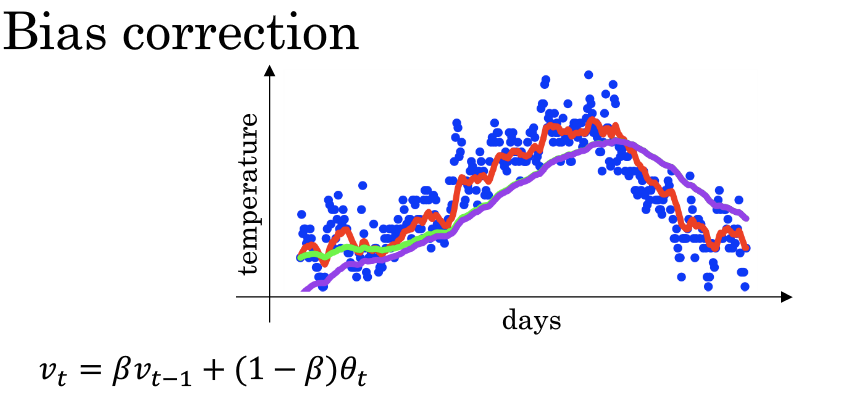
指数加权平均公式:\[V_{t}=\beta V_{t-1}+(1-\beta)\theta_{t}\]
带修正偏差的指数加权平均公式:\[\hat{V}_{t}=\frac{V_{t}}{1-\beta^{t}}=\frac{(\beta V_{t-1}+(1-\beta)\theta_{t})}{1-\beta^{t}}\]

补充
在机器学习中,在计算指数加权平均数的大部分时候,大家不太在乎偏差修正,大部分宁愿熬过初始阶段,拿到具有偏差的估测,然后继续计算下去.
如果你关心初始时期的偏差,修正偏差能帮助你在早期获得更好的估测